This is an article that focusses on one of the most characteristic and stylistically important aspects of French Baroque (and galant) performance practice: inégalité (inequality) and its notes inégales (unequal notes). A considerable number of historical sources point out that, when interpreting French Baroque (and galant) music, inégalité is the norm and that failing to apply it, would result in a performance that lacks the required grace and taste.
Inégalité is a typical French performance practice feature from the 17th and 18th centuries characterized by an unequal interpretation of the smallest notes resulting in note pairs. Uneven notes are played beyond their notation while even notes are played later than their notation and are shorter.
In this article, I will explain how inégalité works, how notes inégales work, and I will give the basic rules as they were given by the masters of the French Baroque and galant periods. As will be illustrated, these rules depend on the time signature, the musical context, and the personal taste and view of the writer and musician.
The Omnipresence of Inégalité (Inequality)
The practice of inégalité and notes inégales is well documented in Baroque and galant French dictionaries, prefaces to editions, tutors and treatises. As Stephen Hefling points out, inégalité “is discussed by more than forty French writers from the latter half of the seventeenth century until the Revolution” (Hefling, Rhythmic Alteration, ix). These sources stipulate that inequality was not optional but must be part of every performance by default. In fact, inequality was so omnipresent that a rhythmically equal execution of the smallest regular notes was an exception and needed to be asked for in the score by means of a written indication or guideline.
How Does Inégalité Generally Work?
Let us first look and listen to the common way of playing notes inégales. The musical example below shows a fragment of a composition written by François Couperin (1668–1733), the beginning of his Allemande à deux Clavecins (Allemande for two harpsichords), opening the ninth Ordre (his term for what another composer might have called a suite) from his second book of harpsichord pieces. (Couperin was a French harpsichordist, organist, and composer best known today for his four books of harpsichord pieces. He was undoubtedly the most important member of a musical dynasty of professional composers and musicians. To distinguish him as such, he received the epithet le Grand (the Great). And as we will see below, Couperin also commented on the practice of inégalité/notes inégales.)

Have a look first at the score and observe the (rhythmically equal notation of the) sixteenth notes.

available on https://imslp.org
Listen now to the wonderful performance of my ex-student Korneel Bernolet, who is also quite the wizard with computers and recording gear, playing here both harpsichord parts:
Korneel’s performance illustrates beautifully how the sixteenths are not played ‘literally’ but with a certain ‘swing’.
More Specific Guidelines on How and When to Apply Inégalité?
Now that we have seen how inequality works in a general way, let us dig somewhat deeper and investigate more specific guidelines as to how and when it should be applied.
1/ Relationship with Time Signature
There was a clear relationship between the time signature and the note values to be played unequal. The following guideline can serve as a rule of thumb:
- In binary time signatures, inequality applied to the fourth part of a beat (for instance, sixteenths in a 4/4 time signature, as illustrated by Korneel’s performance).
- In ternary time signatures, inequality applied to the half-beat. Via this link https://www.youtube.com/watch?v=0XQbQXG-e0s&t=56s, you can listen to a performance of the example below, an excerpt from the famous Passacaille from the opera Armide composed by Jean-Baptiste Lully (1632–1687). (Lully, born in Florence, became the most influential composer of his time at the court of Louis XIV.) This piece is written in a 3(/4) time signature in which the eighth notes are played unequally.

available on https://imslp.org
2/ Variability
Depending on the musical context and the taste of the writer, inequality could vary from barely perceptible (with a ratio of 7:5), over mild (with a ratio of not more than 2:1) and moderate (with a ratio of approximately 3:1) to strong (with a ratio of more than 3:1). Korneel’s performance of Couperin’s Allemande for two harpsichords illustrates well the milder form of inégalité, which seems to have been the common French manner of playing notes inégales. In this case, Korneel plays notes inégales with a ratio that is overall smaller than 2:1. The fact that this ratio is impossible to write down and that the exact degree of inégalité is even within one piece not fixed but variable according to the musical content and the taste of the performer, might be important factors in explaining the discrepancy that existed between the rhythmically equal notation and the rhythmically unequal performance. An early attempt to describe the mild form of inégalité somewhat more concretely was made by the French organist and composer Guillaume-Gabriel Nivers (ca. 1632–1714). In the preface of his Livre d’Orgue (Organ Book) from 1665, he explains that the addition of demipoints (half dots) to the uneven notes of group of eighth notes during the performance results in quite a cheerful mood. He refers, amongst others, to the fugue on page 14 as a good example of this type of inequality. The example below shows the beginning of that fugue. Via this link (https://www.youtube.com/shorts/zkY7vtXvBHM) you can listen to a performance of this piece. Note, however, that the interpreter decided on a type of inégalité that is more pronounced, rather of the 2:1 ratio type than with the addition of (only) demipoints to the uneven eighth notes.

available on https://imslp.org
Whereas writers warn quite often against making inégalité too sharp, sharp inequality did exist as a particular form of inégalité separate from the more regular inequality, at least for some. Those writers state that, to obtain this sharp inequality, composers should effectively write dotted rhythms instead of notes of equal length. One of those writers is the Parisian maître de musique (music master) Étienne Loulié (1654–1702). In his Éléments ou Principes de Musique from 1696 he explains that there are four different ways to perform the smallest regular notes in ternary time signatures, the third of which is the sharpest form of inequality but one in which the uneven notes must be written with a dot. This is how Loulié formulates it:
“There is still a third way, in which one makes the first half-beat much longer than the second, but the first half-beat must have a dot. One calls this third way Piquer, or Pointer.”

Note that the often problematic terminology used by 17th– and 18th-century French writers to indicate different types of inequality is dealt with in my article Historical Terminology to Indicate Inégalité (Inequality).
There are also some writers who allow written notes of equal length to be performed with this sharp inequality that for Loulié must be marked in the score by actual dotted rhtyhms. One of those writers is Monsieur de Saint Lambert (fl 1700). (Saint Lambert, whose first name remains unknown, was a French harpsichordist, composer and teacher.) In his Principes du Clavecin from 1702, he states the following:
“When one must render eighth notes or quarter notes unequal, it depends on one’s taste to decide whether they must be somewhat or strongly inégales. There are pieces where it fits well to render them strongly unequal, and other ones where they want to be less so. The taste is the judge of that just as of the tempo/character.”

public domain, available on https://imslp.org; my translation
3/ Inequality Exclusively for Notes Moving by Stepwise Motion?
At least 13 treatises seem to prescribe or imply inégalité/notes inégales only for notes moving by stepwise motion, prescribing a rhythmically equal performance the same type of notes moving by leap. As Hefling mentions, six of those sources mention this distinction verbatim (Hefling, Rhythmic Alteration, 12). One of those six treatises is François Couperin’s L’Art de toucher Le Clavecin (‘The Art of Playing the Harpsichord’), a treatise on harpsichord performance practice Couperin published in 1716 and republished one year later, in 1717, in a revised version. Observe how Couperin refers here to the practice of notes inégales in the context of stepwise motion, showing a certain frustration as to the difference between notation and performance as well:
“In my view there are defects in our way of writing music, which correspond to the manner of writing our language. It is that we write differently than we play: which causes foreigners to play our music less well than we play theirs. By contrast the Italians write their music in the true values in which they conceived it. For example, we point several eighths that proceed by conjunct degrees; however, we mark them equal; our custom has enslaved us; and we continue.”


public domain, available on https://imslp.org;
translation from Hefling, Rhythmic Alteration, p. 12
Historical evidence, however, seems to suggest that this must not have been a hard rule. Indeed, there are sources in which leaping notes are prescribed to be played unequally. A clear example of this practice can be seen in the treatise L’École d’Orphée from 1738 written by Michel Corrette (1707–1795). (Corrette was a French composer, organist and author.)
“The time signature with four beats indicated with a C is very useful for church music, and is widely used in Italian music, as in the allemandes, adagio, allegro, andante, presto of the sonatas and concerto. One plays the eighth notes equally, one should play the second sixteenth note faster. See page 30.”

available on https://imslp.org; my translation

available on https://imslp.org
The example above illustrates that, according to Corrette in this treatise, both leaping sixteenth notes as sixteenths notes moving by stepwise motion should be played unequally.
A later example illustrating that inégalité was not limited to notes moving by stepwise motion is La Chanson des Marseillois as notated in an early edition from the year of its composition, 1792. In fact, La Chanson des Marseillois —a war song written by Claude-Joseph Rouget de Lisle (1760–1836)— would become the French national anthem or La Marseillaise.

While most of us are quite familiar with the sharply dotted rhythms of this anthem (for those who aren’t, you can listen to it via https://www.youtube.com/watch?v=FTIk66b3dds), not only the leaping notes but also the repeated notes are written as equal eighth notes in the fragment from the edition above. It was only in the 19th century that editors of La Marseillaise effectively started writing dotted rhythms.
Two Special Cases
1/ The Short-Long Inégalité
As we have seen above, the standard way of performing notes inégales is by lengthening the uneven notes beyond their written value, making the even notes shorter by having them start later (the long-short inequality). Yet a number of writers also give the possibility of the opposite rhythmic pairing, that is with the uneven notes that are shorter than their actual notation and the even notes that are longer and start earlier than their actual notation (the short-long inequality). The most known examples of this type of inequality occur in the ornament table and works of François Couperin, who foresaw a specific notation for the short-long inequality. Below you can observe that notation as well as the explanation of this type of inégalité from Couperin’s ornament table:
“Slurs, wherein the dots indicate that the second note of each beat must be stressed/lengthened more.”

available on https://imslp.org;
modified translation from
Hefling, Rhythmic Alteration, p. 14
It must be pointed out, however, that this short-long inequality, today usually called Lombardic rhythm, remained the exception and needed to be stipulated by the composer. Consider the next example by Couperin, an excerpt from the beginning of Les Moissonneurs (The Reapers), opening the sixth Ordre.

Here is a link to listen to it: https://www.youtube.com/watch?v=fpLpEjcnjWI.
Observe that Couperin uses his special notation to indicate short-long inequality only in relation to three groups of four eighth notes in the first couplet and two groups of four eighth notes in the second couplet (no such indication occurs in the third couplet). This strongly suggests that, as the performer also does in the link given above, all the other eighth notes should be played in the ‘normal’ way, that is, with long-short inequality.
2/ Inégalité Transferral and Cumulative Inégalité
As mentioned above, a time signature was generally related to one type of note value —the smallest, regularly appearing note value— that needed to be rendered unequal (for instance, sixteenths in a 4/4 time signature). Occasionally, however, a smaller note value takes prominence in a piece. In this case, the sources agree on the fact that this smaller note value needs to be rendered unequal. They do not agree, however, on how to treat the usual notes eligible for inequality. As Hefling pointed out, “treatise writers who address this matter fall into two groups: those for whom inequality descends, and those who postulate that it is cumulative” (Hefling, Rhythmic Alteration, p. 27).
Hyacinthe Azaïs (1741–1796), a French composer but mainly teacher, shows himself quite critical of the relationship between a time signature and specific notes to render unequal. In his Méthode de Musique Sur un nouveau Plan from 1776 he expresses the view that inequality counts simply for the smallest note values, regardless of the time signature:
“The law of equality or inequality has nothing in common with the correct or faulty manner of indicating a meter. This law is derived from the simple but general principle that it is always the notes of least value employed in a measure that are rendered unequal.”

On the other hand, in his Musique Théorique Et Pratique from 1722, Borin (fl 1722–1746) belongs to those who hold the view that inequality accounts not only for the usual notes, but also, the case being, for smaller note values. (I did not find any biographical information on Borin, not even his first name.)
“Cut time is beaten in two, two quarter notes or the equivalent are required for each beat, the eighth notes are unequal; & consequently the sixteenths, because one should observe that in whatever time signature, when one type of notes is unequal, it follows that the smaller types are too.”

available on https://www.bnf.fr/fr; my translation.
Hefling rightly points out that cumulative inequality “would surely produce unusual rhythmic clashes in keyboard or ensemble music, but none of the sources mentions such a problem” (Hefling, Rhythmic Alteration, p. 27).
Cancelling Inégalité
Since inégalité was the norm and omnipresent, nothing needed to be marked in French scores to ensure its inclusion whilst performing. When a composer, however, wanted the notes that are usually played unequally to be played equally, he/she needed to make that clear by some kind of indication in the score. The cancellation of inequality could be asked for by a number of means, of which the two most common ones are dots or small vertical lines and the verbal indication notes égales.
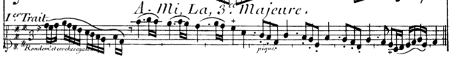
available on https://imslp.org

public domain, available on https://imslp.org
Further Reading (Selection):
1/ Primary Sources
- Azaïs, Hyacinthe. Méthode de Musique Sur un nouveau Plan (Sorèse, 1776).
- Borin. La Musique Théorique Et Pratique (Paris, 1722).
- Corrette, Michel. L’Ecole d’Orphée (Paris, 1738).
- Couperin, François. L’Art de toucher Le Clavecin (Paris, 1716 and 1717).
- Hotteterre, Jacques-Martin. L’Art de Préluder sur la Flûte Traversière (Paris, 1719).
- Loulié, Étienne. Éléments ou Principes de Musique (Paris, 1696).
- Nivers, Guillaume-Gabriel. Livre d’Orgue (Preface) (Paris, 1665).
- Saint Lambert, Monsieur de. Principes du Clavecin (Paris, 1702).
2/ Secondary Sources
- Byrt, John. Some New Interpretations of the Notes Inégales Evidence, in: Early Music 28/1 (2000), 99–112.
- Demeyere, Ewald. Johann Sebastian Bach’s Art of Fugue — Performance Practice Based on German Eighteenth-Century Theory (Leuven: Leuven University Press, 2013).
- Fuller, David. Notes inégales (Grove Music Online. 2001; Accessed 8 Oct. 2022), https://www.oxfordmusiconline.com/grovemusic/view/10.1093/gmo/9781561592630.001.0001/omo-9781561592630-e-0000020126.
- Hefling, Stephen E. Rhythmic Alteration in Seventeenth- and Eighteenth-Century Music: Notes Inégales and Overdotting (New York: Schirmer Books, 1993).
- Kuijken, Barthold. The Notation Is Not the Music — Reflections on Early Music Practice and Performance (Bloomington: Indiana University Press, 2013).
